Franklin Monteiro Molitor
Escolha do Tema
A escolha deste tema decorre de uma necessidade que o pesquisador teve em sua prática como professor. O mesmo procurava um texto que continha mais do que as propriedades básicas do triângulo aritmético e também demonstrações matemáticas rigorosas de cada uma delas.
A carência de bibliografia em português deste tema também foi um fato que despertou a atenção do pesquisador, sendo incentivado para o presente trabalho.
Quando ministrava aulas de análise combinatória e probabilidade, o pesquisador apresentava o triângulo aritmético e observava como os alunos viam com certo espanto os resultados que se encontravam nele, até mesmo os alunos menos interessados faziam muitas perguntas. Perguntavam como algumas sequências apareciam, várias vezes o pesquisador explicava, mas outras vezes tinha que assumir que não sabia. Perguntavam também se haviam mais propriedades além daquelas apresentadas, se haviam outras e se poderiam haver outras que ninguém ainda tinha descoberto. Isso fornece uma perspectiva ao aluno e aos outros envolvidos no processo, como professores, que a matemática não é algo pronto e acabado, resultado da construção humana, que ainda é possível fazer novas descobertas, mesmo na atualidade.
O que é o triângulo aritmético?
O triângulo aritmético é bastante conhecido historicamente por conter muitos padrões numéricos como sequências, somatórias, combinações, coeficientes binomiais etc. Ele funciona a principio como uma brincadeira com aritmética, ou seja, com a operação da soma.
Toma-se um elemento gerador, que normalmente é o número 1, mas pode-se usar qualquer número. Cada elemento deve ser a soma dos dois elementos que estão logo acima dele, se não houver dois elementos ele deve ser igual ao elemento gerador.

Triângulo Aritmético
Ele foi amplamente estudado por Blaise Pascal no século XVII, porém ele é conhecido pelos chineses desde o século XIII, que já o consideravam um triângulo mágico por conter números muito complicados de se calcular na época.
Dissertação
Esta dissertação está dividida em três partes:
1 - Estudo detalhado do Tratado do Triângulo Aritmético de Pascal de 1654 com uma modernização da linguagem matemática e uma abordagem mais rigorosa nas demonstrações de suas propriedades contendo: 19 consequências e 01 problema; Ordens Numéricas; Combinações; Divisões de apostas em jogos; Potências de Binômios.
2 - Propriedades: Combinação; Relação das Diagonais; Sequência de Fibonacci; Sinais Alternados; Números Figurados e Piramidais; Potência de Binômios e Trinômios; Partição de Combinações; Matriz de Pascal; Forma Quadrática; Plano Aritmético.
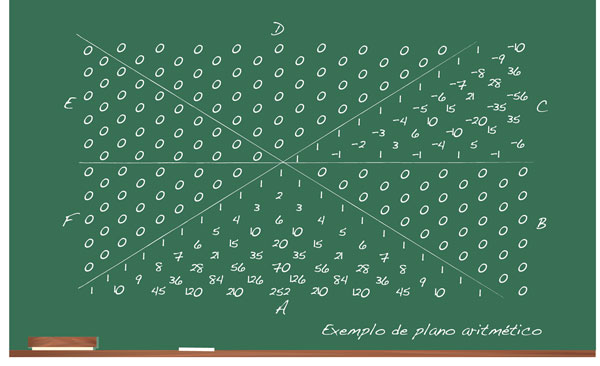
3 - Um plano de aula contendo o enunciado das propriedades com métodos de preparo de uma apresentação aos alunos com justificativas em linguagem simples para que a aula fique mais dinâmica e interessante. Pode ser lido tanto por professores quanto por alunos mais avançados.
Perfil

Nome: Franklin Monteiro Molitor
Graduação: Licenciatura em Matemática – Universidade de São Paulo
Pós-Graduação: PROFMAT – Universidade Federal do ABC
Trabalho Atual: Professor de Matemática na ETEC Parque da Juventude, São Paulo
