Um breve ensaio sobre leis físicas elegantes (V.4, N.3, P.7, 2021)
Tempo estimado de leitura: 8 minute(s)
Divulgador da Ciência:

Figura 1. Camiseta com as equações de Maxwell [1].
É relativamente fácil comprar camisetas com equações e referências a Deus (sim, O Deus). Pensando a respeito, cheguei a várias conclusões interessantes, sendo que a mais relevante é que algumas equações conseguem vender camisetas e outras não. É sobre esse assunto que trata este ensaio.
Na figura 1, apresentamos uma camiseta com as famosas equações de Maxwell na sua forma diferencial. Famosas para os físicos, em particular os amantes da física clássica, ou seja, de um universo contínuo. Para um físico, é impossível não ficar maravilhado pela simplicidade e elegância destas expressões. E, além disso tudo, são as bases da tecnologia desde o século XIX.
Reproduzo aqui a versão mais completa das equações de Maxwell em sua forma diferencial, explicitando as constantes de permissividade (ε0) e permeabilidade no vácuo (μ0):
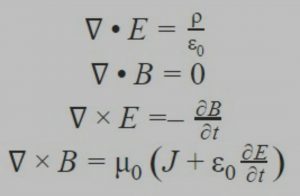
Caro leitor, não se assuste. Imagino que suas dúvidas sejam: o que são estes símbolos? Do que se trata? Qual é o significado dessas quatro linhas misteriosas e criptografadas?
Tudo começou na década de 1860, quando o físico e matemático inglês James Clerk Maxwell publicou artigos ([2][3]) com demonstrações matemáticas sobre como os campos magnético e elétrico interagem e se propagam no vácuo à velocidade da luz. As ondas resultantes destas interações são chamadas de ondas eletromagnéticas: a luz propriamente dita é uma onda eletromagnética.
Comecemos pelos símbolos. Nas equações, o símbolo E representa um campo elétrico, que se manifesta com uma intensidade e uma direção em cada ponto do espaço. Logo, é um campo vetorial, e por isso está representado em negrito. E está presente em três das equações de Maxwell, sendo que apenas na primeira ele está sozinho (sem o B).
Esta (a primeira) equação é conhecida como “Lei de Gauss”. O termo da esquerda (∇.E) é lido como “o divergente de E”, e traduz o fato de as linhas do campo elétrico convergirem ou divergirem. Se as linhas forem paralelas, o valor de (∇ . E) é zero. No caso de uma carga puntiforme, só no ponto onde está a carga o divergente é não nulo (infinito, neste caso!), ao redor ele é nulo. O espaço ao redor de uma carga elétrica positiva tem divergente positivo.
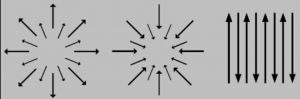
Figura 2. Comportamento do divergente (). À direita, divergente positivo. Centro, divergente negativo. À esquerda, divergente nulo (adaptado de [4]).
O termo à direita da equação é a razão entre a densidade de carga no espaço, , e a permissividade elétrica no vácuo, 0. Esta pequena fração representa a quantidade de carga elétrica no espaço nas unidades adequadas (esse é o papel do 0: essencialmente levar em conta as diferentes escolhas de unidades que podemos fazer para carga e os campos.). Agora, com estas informações, podemos interpretar a primeira equação: dada uma região do espaço com uma certa quantidade de carga elétrica, teremos um campo elétrico saindo de ou entrando nesta região (se a carga for positiva ou negativa). Por outro lado, se não houver carga, não haverá campo elétrico (ρ=0→E=0).
A segunda equação, conhecida como “Lei de Gauss do Magnetismo”, nos fala do campo magnético, B. Essa é mais fácil de interpretar, pois o termo à direita é zero. Aqui temos que o divergente de B é zero, ou seja, as linhas do campo magnético são sempre paralelas e nunca se cruzam.
Neste ponto surge a pergunta: 0 campo magnético pode existir sem a presença de uma “carga magnética”? Essa é uma das respostas a que chegaremos a seguir.
As duas equações seguintes nos apresentam o comportamento dos campos B e E um com relação ao outro. Em outras palavras, como o campo elétrico afeta o campo magnético e vice-versa.
Nos termos à esquerda temos um novo operador, o rotacional, denotado por ∇ x E e ∇ x B . O rotacional nos diz se o campo vetorial dá voltas (se ele “gira”) em uma dada região do espaço. Se as linhas do campo são retas ou divergentes, o rotacional vale zero.
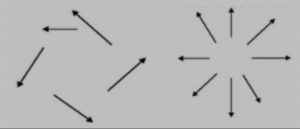
Figura 3. Comportamento do rotacional (). À direita, rotacional não nulo. À esquerda, rotacional nulo (adaptado de [5]).
A outra novidade das duas últimas equações são os símbolos ∂E/∂t e ∂B/∂t, que representam simplesmente a variação de E e de B ao longo do tempo. Se E e B permanecerem constantes, sem alterações, teremos ∂E/∂t=0 e ∂B/∂t=0. Por outro lado, quanto maior for o valor destas grandezas, mais rapidamente os campos estarão variando.
A “equação de Faraday” (a terceira equação) nos diz, portanto, que uma variação no tempo do campo magnético corresponde a uma variação da direção do campo elétrico. Existem algumas regras para determinar o sinal destas operações matemáticas. Nesta equação, o sentido de rotação do campo elétrico é definido pelo valor negativo da variação do campo magnético no tempo.
A última equação é a “equação de Ampère” (com uma pequena modificação incluída por Maxwell). Um símbolo novo é a densidade de corrente, denotado por J. Se imaginarmos a corrente elétrica no interior de um fio condutor, J é a intensidade de corrente dividida pela área da seção transversal do fio. O último símbolo é a permeabilidade magnética no vácuo, μ0, que tem um papel semelhante ao do ε0, como já foi dito mais acima.
Assim, a equação de Ampère modificada nos diz que a curvatura do campo magnético é consequência da presença de corrente elétrica ou da variação no tempo do campo elétrico. O “ou” é devido à soma dentro dos parênteses.
E o que significa tudo isso?
A resposta é a “mágica” do magnetismo
A primeira consequência é que podemos obter resultados magnéticos a partir de efeitos elétricos e vice-versa. Esse é o princípio utilizado nos transformadores, geradores de usinas hidroelétricas, usinas eólicas, usinas termoelétricas, etc. Se incluirmos ainda a expressão da força eletromagnética de Hendrik Lorentz, teremos os eletroímãs e motores elétricos.
A segunda, mas não menos importante ou impressionante, vem do seguinte raciocínio. A variação no tempo de E (ou B) impõe uma variação no espaço de B (ou E). Porém, quando um dos campos se desloca no espaço, isso também corresponde a uma variação no tempo, e o ciclo se repete. A velocidade de propagação destas oscilações acopladas é dada por c=1/√(ε0μ0), a velocidade da luz. E assim temos uma onda eletromagnética (é por isso que eu prefiro a versão com ε0 e μ0 – deixa tudo mais emocionante!).
A verdadeira beleza destas fórmulas está na sua simetria e simplicidade. O entendimento e compreensão destas leis possibilitou a construção de máquinas e equipamentos que definem a sociedade em que vivemos. Elevadores, carros elétricos, telecomunicações, computadores, telefones, liquidificadores, impressoras, luz artificial. Praticamente, todos os confortos que a tecnologia atual nos oferece têm suas bases nas leis de Maxwell. Imagine sua vida sem eletricidade…
Agora entendemos por que a palavra divina foi incluída na camiseta. No início dos tempos, ao proferir as famosas palavras [6], o Criador também nos permitiu fazer uma referência às leis físicas que viriam a ser descobertas em 1860.
Referências
[1] https://www.amazon.co.uk/God-Said-Then-There-Light/dp/B07HG83QHB
[2] Maxwell, J.C., 1861, “On Physical Lines of Force”, Philosophycal Magazine of Journal of Science, 4th series, pp. 166
[3] Maxwell, J.C., 1865, “A Dynamical Theory of the Electromagnetic Field“, Philosophical Transactions of the Royal Society of London 155, 459–512
[4] https://en.wikipedia.org/wiki/Divergence#/media/File:Divergence_(captions).svg
[5] http://fma.if.usp.br/~fleming/vfield/node10.html
[6] Gênesis 3:1.